Давление воды — это force, которую вода оказывает на поверхности, находящиеся в её среде. Оно зависит от глубины, в которой находится объект: чем глубже погружение, тем выше давление из-за веса водяного столба над ним. Давление воды может измеряться в различных единицах, таких как паскали или миллиметры ртутного столба.
Давление воды играет важную роль в природных процессах и технических системах, таких как водоснабжение, гидравлика и океанография. Оно влияет на поведение воды, её способность сжиматься и перемещаться, а также на взаимодействие с другими веществами, что делает его ключевым параметром для изучения не только водных ресурсов, но и экосистем в целом.
Гидростатика
Прежде чем говорить о давлении жидкостей, следует напомнить о самом понятии давления.
Давление – это физическая величина, равная отношению силы, которая действует на некоторую площадку, к площади этой площадки:
F – сила, действующая на площадку [Н]
S – площадь этой площадки [ (м^) ]
Например, если просто давить кончиком пальца на кожу, не получится проделать дыру – палец очень широкий, и нужно приложить большую силу. Но, давя этой же силой на иголку, дырка получится – ведь теперь сила приходится на площадь конца иголки, а она очень и очень маленькая. Аналогично девушка массой 60 кг, стоя в туфлях на каблуках, создает такое же давление, как целый груженный БЕЛАЗ массой 200 т. Разница в массе нивелируется разницей в площади площадки, на которую давят.
Согласно этой формуле, жидкость также своей массой может оказывать давление на дно сосуда, в который она налита. Если заменить давящую силу силой тяжести mg, а массу жидкости – ее плотностью и объемом, останется лишь заменить объём жидкости его формулой из геометрии. Рассмотрим параллелепипед высотой h с площадью дна S для удобства:
Получается, что любая жидкость оказывает давление на дно сосуда, зависящее только от ее плотности и высоты столба:
Р – давление столба жидкости [Па]
(rho) – плотность жидкости [ (frac>) ]
g – ускорение свободного падения [ (frac>) ]
h – высота столба жидкости [м].
Ширина столба жидкости не важна для создания давления. Поэтому будьте аккуратны – зажать пяткой слив воды в ванной безопасно (так как высота столба считается от слива до дна сифона, это примерно 10 см), а зажать только такой же слив в водонапорной башне высотой 10 м уже смертельно опасно.
Также можно найти среднее давление, с которым жидкость действует на боковую грань сосуда. Для этого достаточно подставить в формулу половину высоты сосуда. Но учтите – среднее давление не равно фактическому давлению в конкретной точке боковой грани. Фактическое давление можно рассчитать, зная глубину погружения этой точки относительно поверхности.
После прочтения предыдущего абзаца возник вопрос – если сила тяжести направлена вертикально вниз, как жидкость давит на боковую грань? Здесь проявляется следствие закона Паскаля – жидкость передает давление на некотором уровне во все стороны. Именно это может привести к гидроудару в квартирах – если резко вернуть жидкость в трубы, она разорвет те трубы, которые были перекрыты кранами.
Важным следствием закона Паскаля является то, что давление внутри жидкости на одной и той же глубине всегда будет одинаково. То есть, если наполнить жидкостью зигзагообразную трубу (как змеевик в квартирах), не важно, что с поверхностью жидкость сообщается лишь в одном месте. Во всех коленах этой трубы давление на одном и том же уровне будут одинаковы.
С газом ситуация аналогична (пример – воздушный шарик, который расширяется во все стороны сразу).
Говоря про изогнутую трубу, мы, по сути, говорили о ряде сообщающихся друг с другом сосудов.
Сообщающиеся сосуды – это взаимодействующие друг с другом сосуды, которые имеют общее дно.
Если рассмотреть сосуды, которые сообщаются друг с другом и с атмосферой (например – стакан с соломинкой) можно заметить важное свойство – уровень одной и той же жидкости в них идентичен. Это возможно именно благодаря атмосфере – она давит на жидкости в сосудах до тех пор, пока уровень давления (а стало быть, и высоты) в них не установится равным атмосферному.
Если в один сообщающийся сосуд налить новую жидкость в дополнение к старой (в стакане с соломинкой была вода, а вы добавили в стакан немного масла), то уровни жидкости в сосудах изменятся, и больше не будут одинаковы. Но главное правило сообщающихся с атмосферой сосудов сохранится – давление в каждом сосуде будет равно атмосферному, или проще говоря – давление в каждом сосуде будет одинаково. При этом уровень, относительно которого проводятся расчеты, можно выбрать в любой части сосудов.
Это принцип сообщающихся сосудов – давление жидкостей на один и тот же уровень в сообщающихся сосудах одинаково, несмотря на разную высоту столбов жидкостей. Но если в сосудах налита одна и та же жидкость, уровень жидкости в сосудах тоже будет одинаковым.
Пример со стаканом с соломинкой выбран не просто так, ведь почти каждый хоть раз использовал такой девайс. Но как он работает? Все просто – когда вы хотите потянуть напиток через соломинку, вы создаете во рту недостаточное давление. Тогда напиток из стакана, на который давит атмосфера, начинает течь через соломинку – ведь давление в сообщающихся сосудах должно быть одинаково.
Высота столба в соломинке растет, а вместе с ним по формуле (texth) растет его давление, и напиток попадает в рот. Но возможно обратная ситуация – пустить через соломинку пузырь. Для этого нужно создать в соломинке избыточное давление – тогда уровень жидкости в ней будет падать, чтобы скомпенсировать его, пока воздух не дойдет до конца соломинки.
Если теперь взять два сообщающихся открытых сосуда, а потом один запаять – получится почти тоже самое. Только теперь вы не управляете воздухом в запаяной части, не можете повысить или понизить его давление.
Этот воздух управляет уровнем жидкости в запаяной части – если воздух давит сильно, высота жидкости в этой части падает, пока не сможет уравновесить давление воздуха, и наоборот, когда воздух давит слабо. Но отчего зависит, как сильно давит воздух в запаяной части? Давление в сообщающихся сосудах должно быть одинаково в обеих частях, значит давление запаяной части (и высота столба жидкости в нём) зависит от давления в незапаяной части, которая сообщается с атмосферой. Получается, именно атмосфера определяет, какова будет высота столбца жидкости в запаяной части. И таким образом был создан первый барометр.
Источник3: www.webmath.ru
Гидростатическое давление
Физическая величина, равная отношению нормальной силы ($F$), действующей со стороны жидкости на некоторую площадь, на величину этой площади ($S$) называют давлением ($p$) жидкости:
Если несжимаемая жидкость находится в равновесии давление по горизонтали всегда одно и то же. Свободная поверхность жидкости всегда горизонтальна, за исключением места около стенок сосуда. У несжимаемой жидкости плотность не зависит от давления. Если поперечное сечение цилиндрического столба жидкости равно $S$, высота столба $h$, плотность жидкости $rho $, тогда вес ($P$) этого столба равен:
[P=rho gSh left(2right).]
В соответствии с (1) давление на основание столба жидкости составит величину:
Формула (3) указывает, что давление столба несжимаемой жидкости на дно сосуда зависит от высоты и плотности жидкости. В общем случае плотность зависит от температуры жидкости. Давление, которое вычисляется при помощи формулы (3) называют гидростатическим давлением/
Определение
И так, гидростатическим давлением называют давление столба жидкости, находящейся в состоянии равновесия, над некоторым условно выбранным уровнем при действии силы тяжести. Гидростатическое давление определяется по формуле (3).
Давление внутри жидкости ($p$) на глубине $h$, будет складываться из давления атмосферы ($p_0$) и гидростатического давления:
Единицей измерения гидростатического давления в Международной системе единиц (СИ) является паскаль (Па):
Закон Архимеда
В соответствии с формулой (3) давление, оказываемое на нижние слои жидкости больше, чем на верхние. Из-за этого тело, погруженное в жидкость, испытывает действие выталкивающей силы. Величину выталкивающей силы определяет закон Архимеда: На тело, находящееся в жидкости (газе) действует выталкивающая сила, которая равна весу жидкости (газа) вытесненной телом. Эта сила называется силой Архимеда ($F_A$):
[F_A=rho gV left(4right),]
где $V$ — объем тела; $rho $ — плотность жидкости; $g$ — ускорение свободного падения. Сила Архимеда направлена вверх.
Примеры задач с гидростатическим давлением
Пример 1
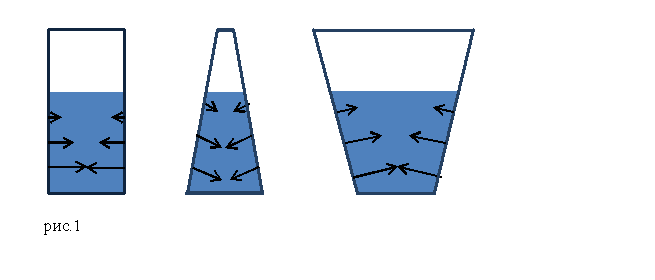
Задание. В чем состоит суть гидростатического парадокса?
Решение. Гидростатическим парадоксом называют явление, при котором сила весового давления жидкости, находящейся в сосуде отличается от веса находящейся там жидкости. Сила давления жидкости на дно емкости равняется весу жидкости только в том случае, если сосуд имеет форму цилиндра. При такой конфигурации емкости стенки являются вертикальными, силы давления стенок на жидкость (соответственно, жидкости на стенки) направлены горизонтально, вертикальной составляющей они не имеют (рис.1).
Если сосуд имеет вверху поперечное сечение больше, чем сечение дна, то сила давления на дно меньше, чем вес жидкости. И наоборот, если сосуд с жидкостью имеет сужающееся вверху горло, то сила давления на дно сосуда больше, чем вес жидкости.
Причиной возникновения гидростатического парадокса является то, что жидкость оказывает давление не только на дно сосуда, но давит и на его стенки. При этом давление на стенки сосуда, расположенные не перпендикулярно основанию имеют вертикальную составляющую. При этом в сосуде, который расширяется к верху, эта составляющая направлена вверх, а в сосуде, уменьшающем свое сечение к верху, вертикальная составляющая давления направлена вниз. Вес жидкости вычисляется как сумма всех вертикальных компонент давления жидкости по внутренней площади емкости.

Пример 2
Задание. Каково гидростатическое давление воды на дно сосуда с водой, если высота столба жидкости составляет $h=$0,5 м?
Решение. Гидростатическое давление на дно сосуда найдем как:
[p=rho gh left(2.1right),]
Вычислим это давление:
[p=1000cdot 9,8cdot 0,5approx 5000 (Па)]
Ответ. $papprox 5000$ Па

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 463 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Остались вопросы?
Здесь вы найдете ответы.
Источник4: www.webmath.ru